MONDAY, 25 MAY 2020
The solutions of Einstein’s field equations of general relativity are known as spacetimes and describe hypothetical geometries of our universe, but the question as to which spacetime we exist in is still up for debate in physical cosmology. An ongoing debate relates to whether we exist in a positively curved or flat spacetime (two-dimensional examples are shown in Figure 1); in addition, there exists a hypothetical spacetime that has negative curvature everywhere. This is known as anti-de Sitter space.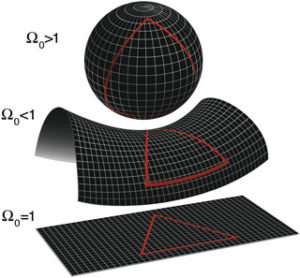 Figure 1: Two-dimensional interpretation of positively curved (top), negative curved (middle) and flat (bottom) spacetime.
Figure 1: Two-dimensional interpretation of positively curved (top), negative curved (middle) and flat (bottom) spacetime.While it is not thought that the spacetime in which we exist is AdS, one theory states that we exist in a spacetime that forms the surface boundary of an AdS space. In this model, particles within the AdS space correspond to particles in our spacetime. Interactions between particles in AdS space therefore place constraints on the corresponding particles in our spacetime. Therefore, as a result of this instability, a black hole formed in AdS space will eventually generate, via Hawking radiation, a shower of particles in AdS space in thermal equilibrium with each other (with no net exchange of thermal energy), and as a result, the corresponding particles in our spacetime are also constrained to also reach thermal equilibrium eventually. This hints at the origin of the second law of thermodynamics, which states that isolated systems spontaneously evolve towards thermal equilibrium.
While the idea of proving instability in a purely hypothetical model may seem abstract, the mathematical tools that Moschidis is developing could also help to illuminate real world phenomena; for example it could help us understand turbulence, which is caused by instabilities that appear in fluid systems, and is poorly understood as of now.
Publication: Georgios Moschidis. A proof of the instability of AdS for the Einstein-massless Vlasov system. arXiv
Figure 1: https://skyandtelescope.org/astronomy-resources/curvature-of-spacece/
News Article: Steve Nadis. New Math Proves That a Special Kind of Space-Time Is Unstable. Quanta Magazine.
Clifford Sia is a fourth-year medic at St.Catharine’s College and website editor at BlueSci. Shamil Shah is an MSci physicist at Jesus College.
